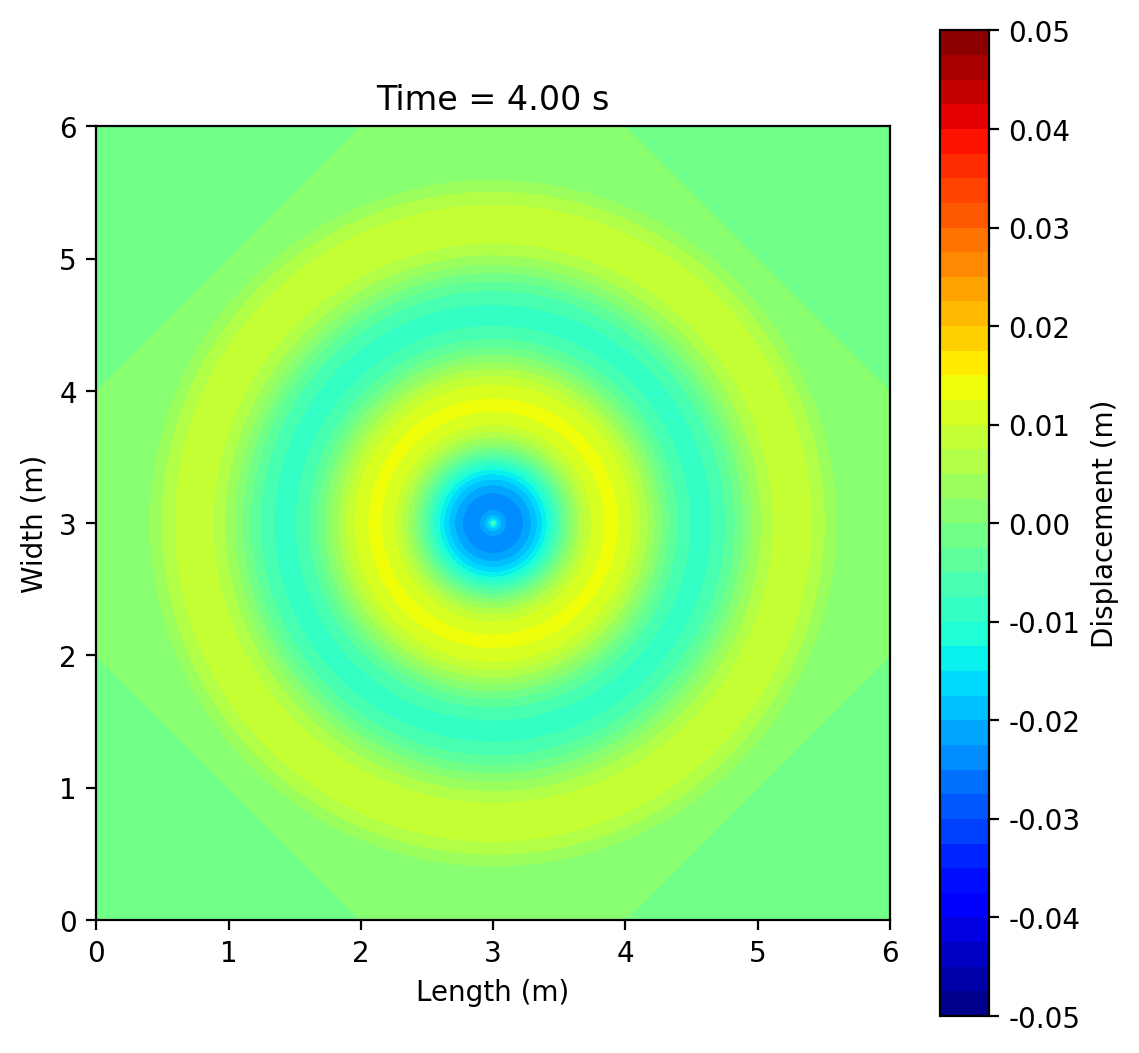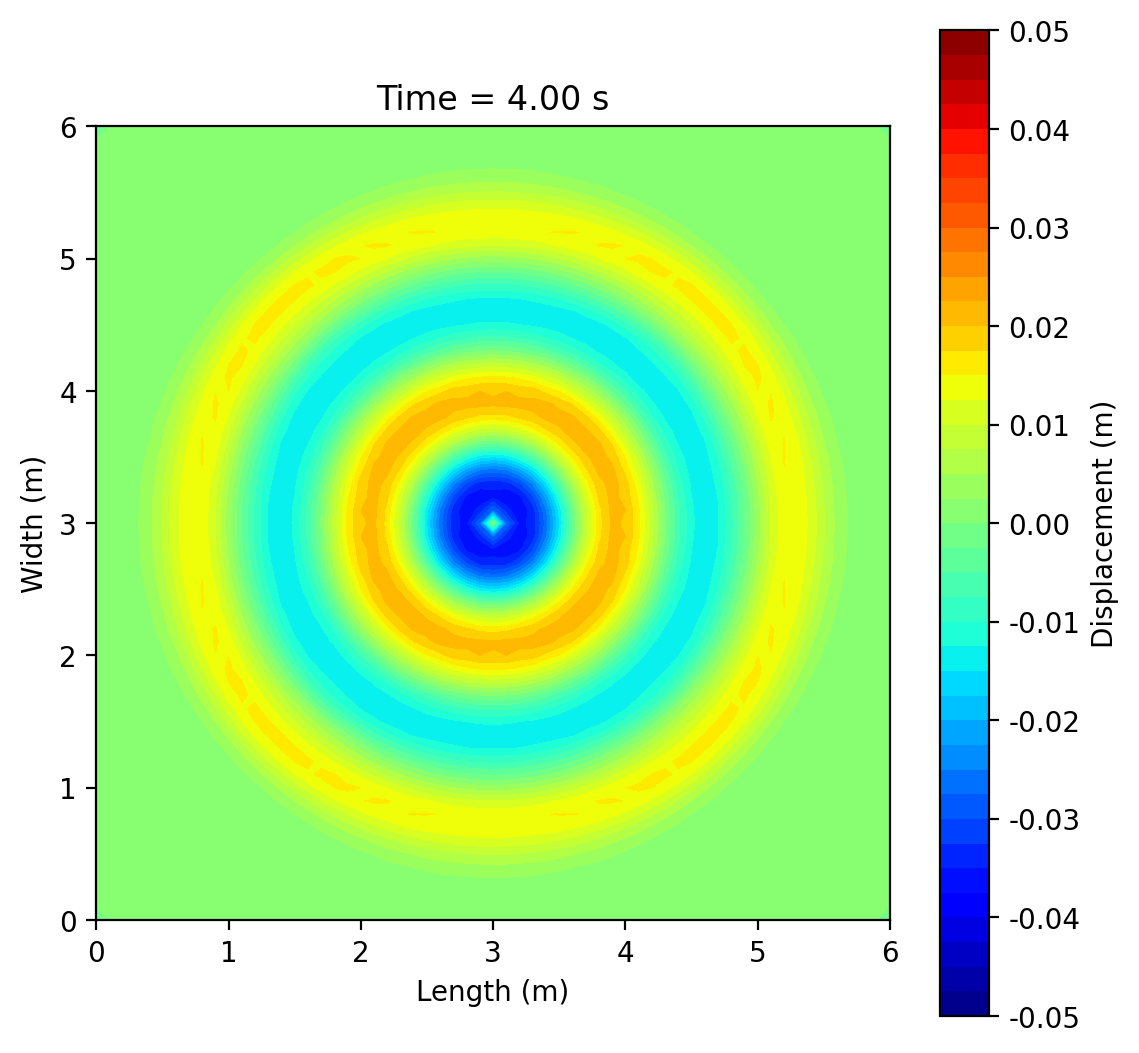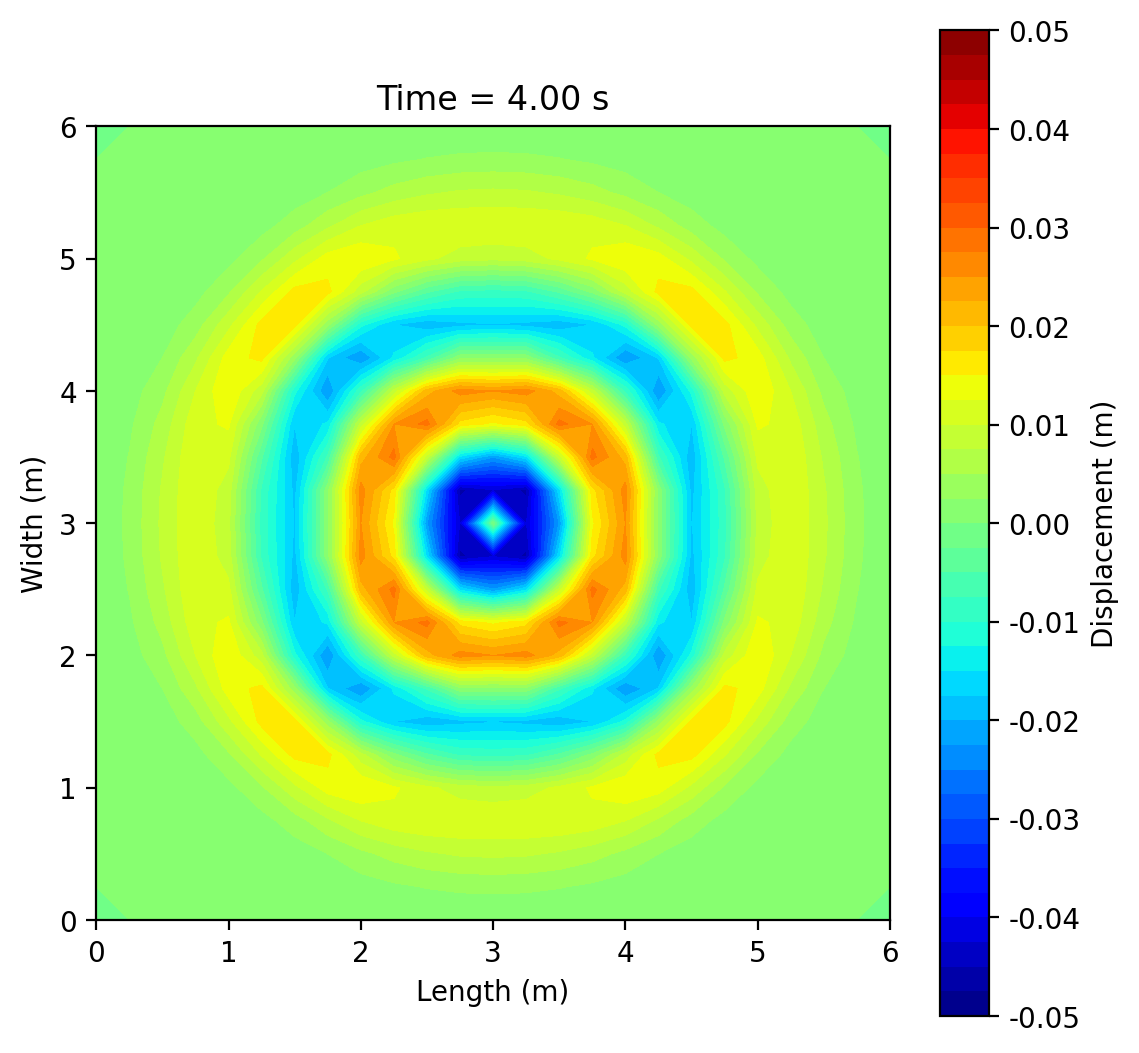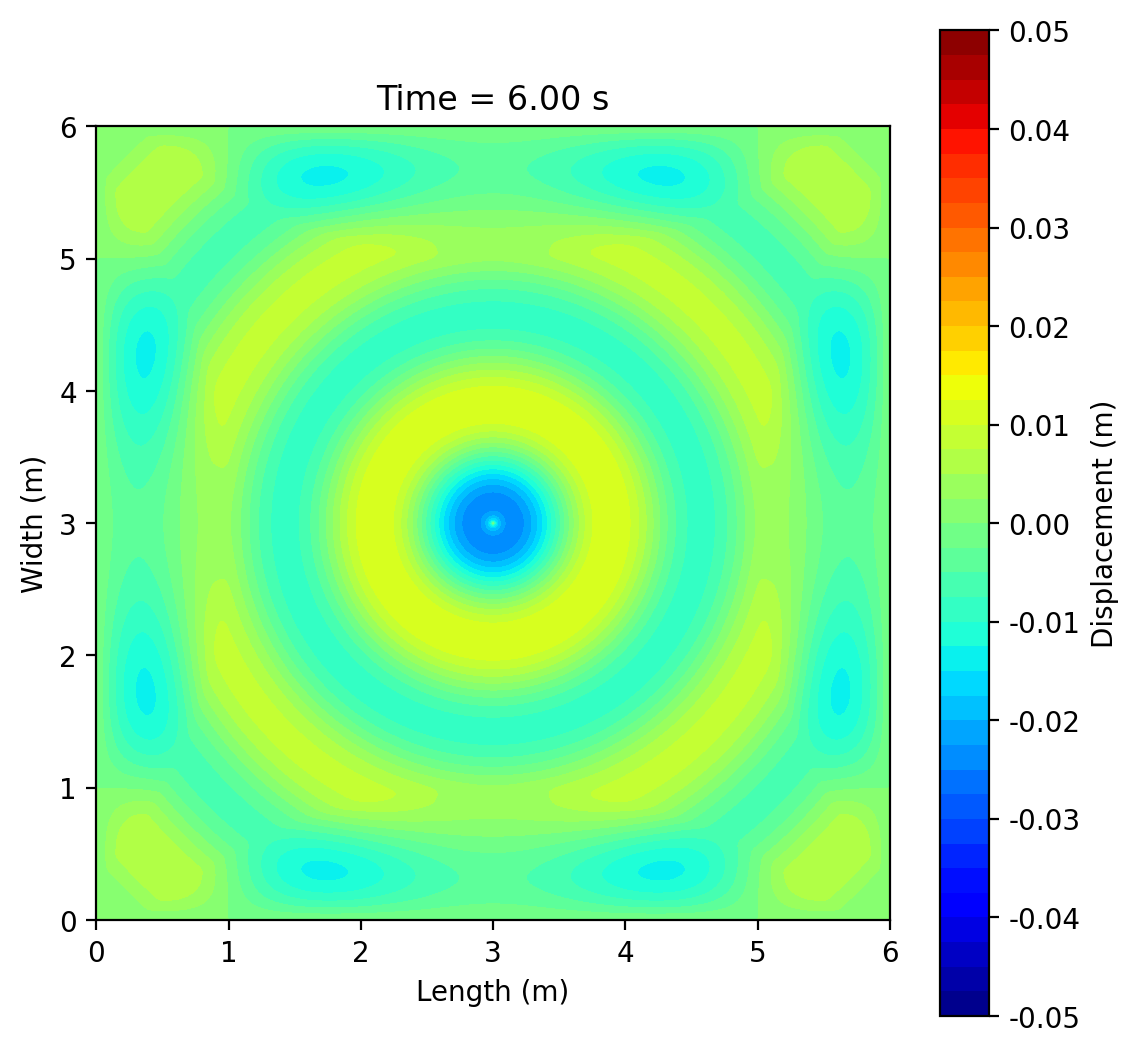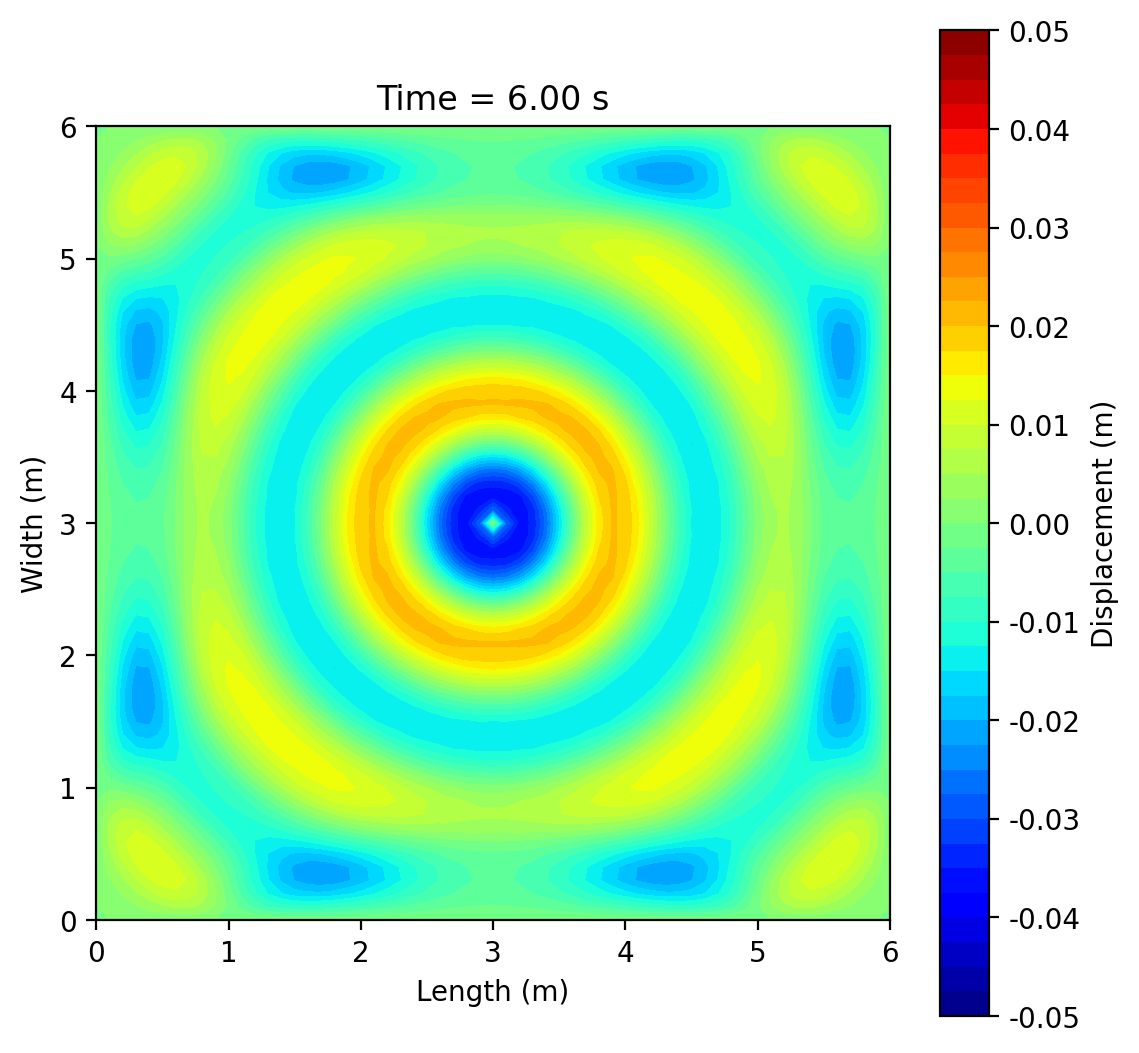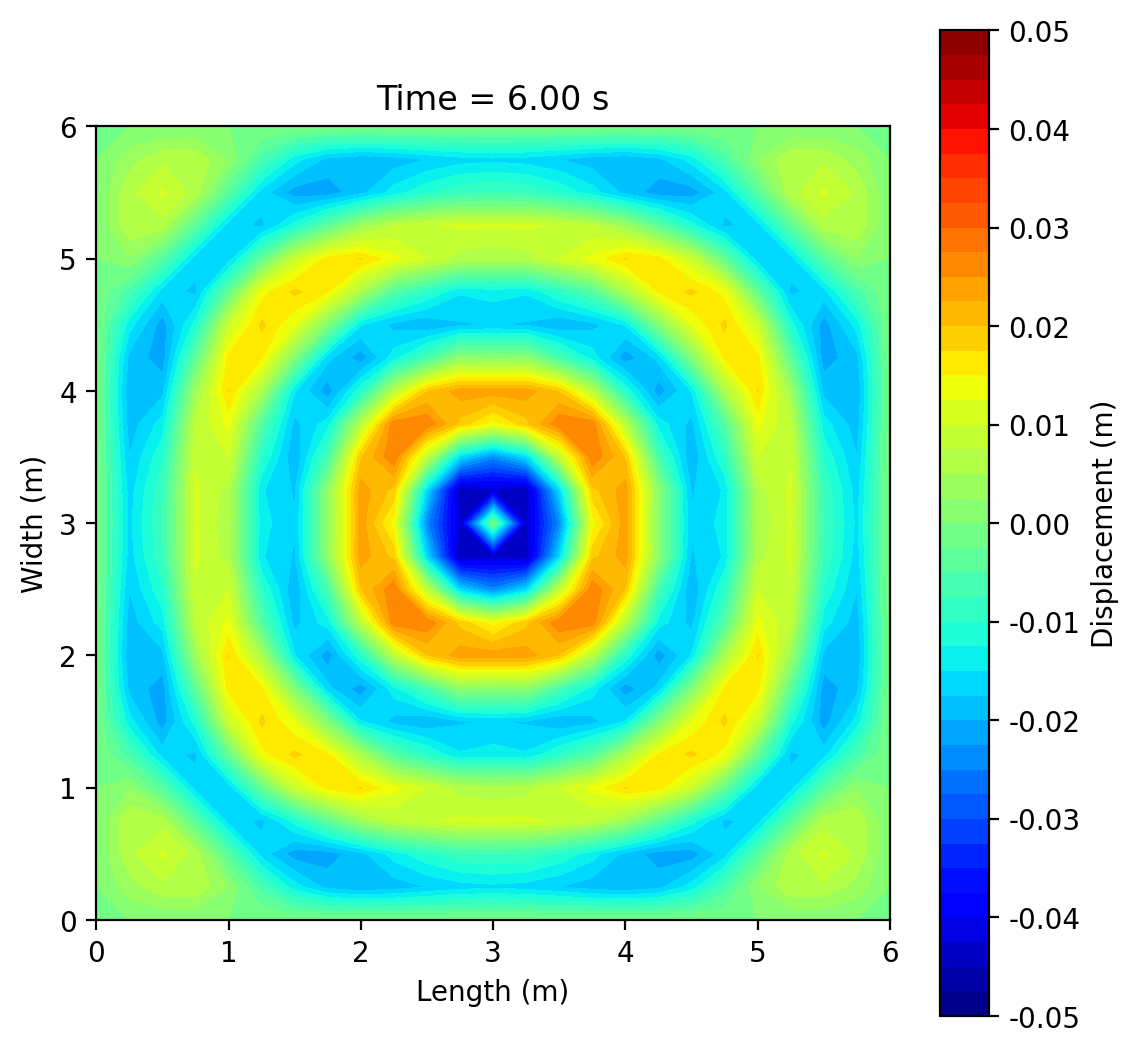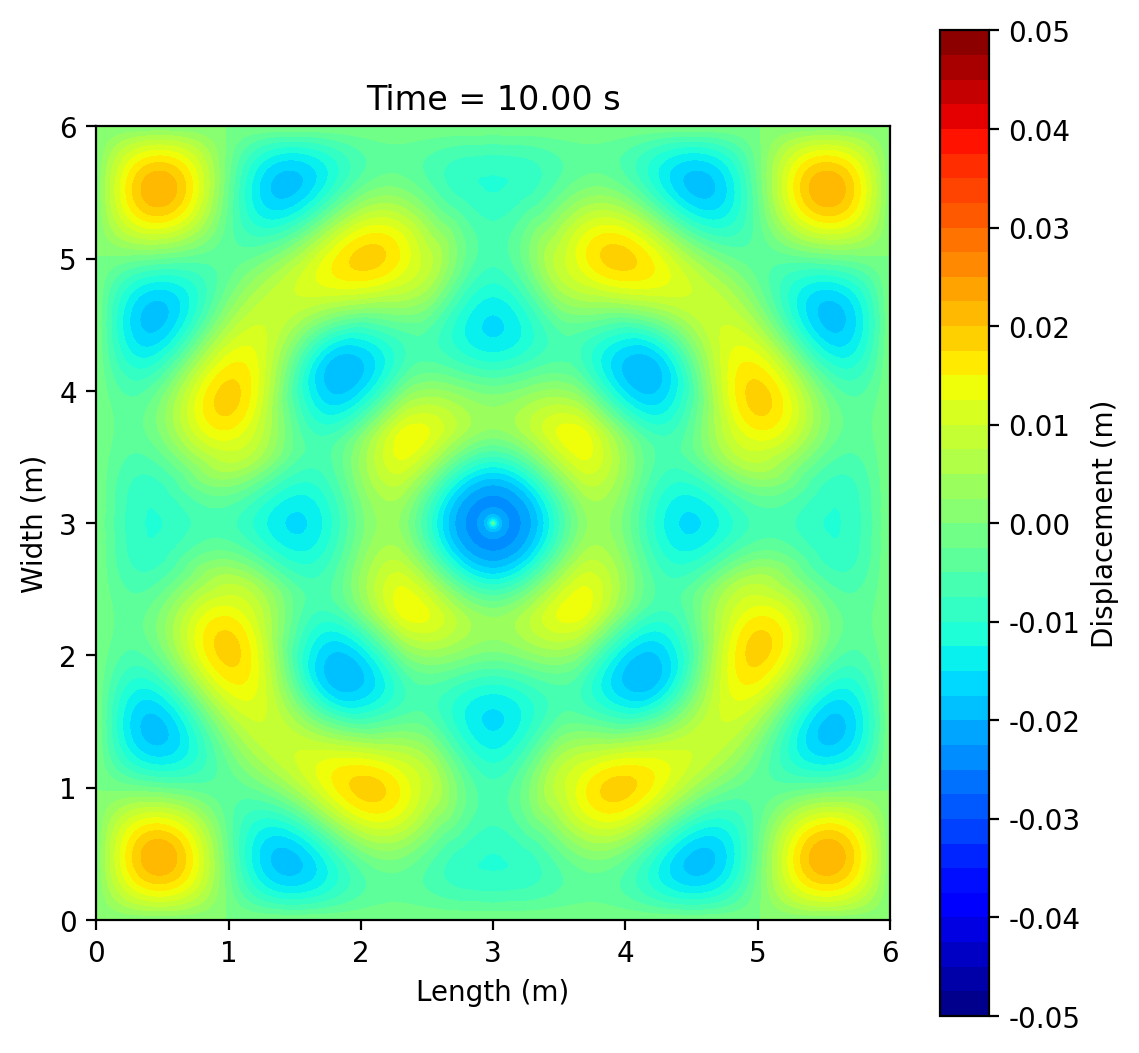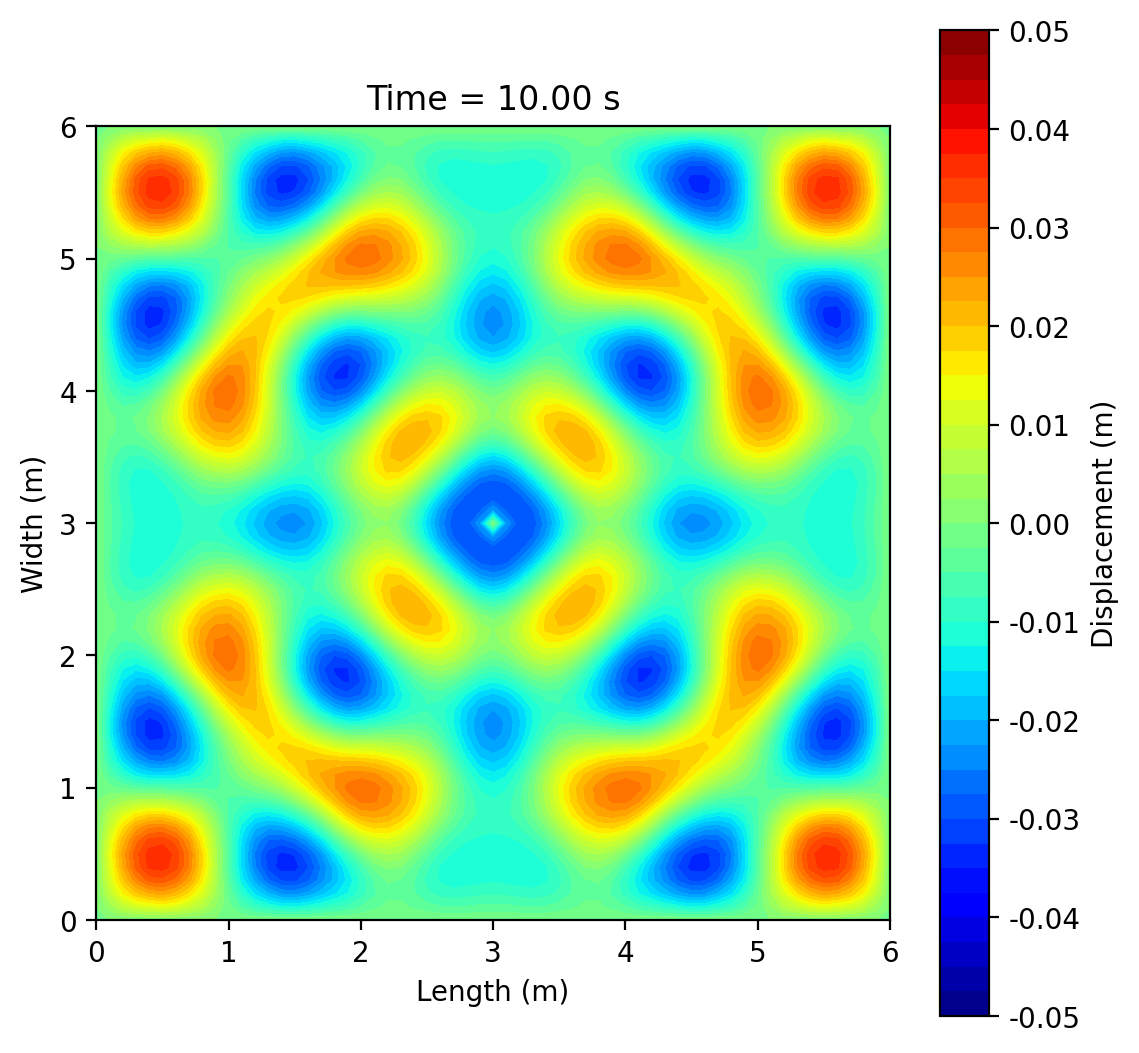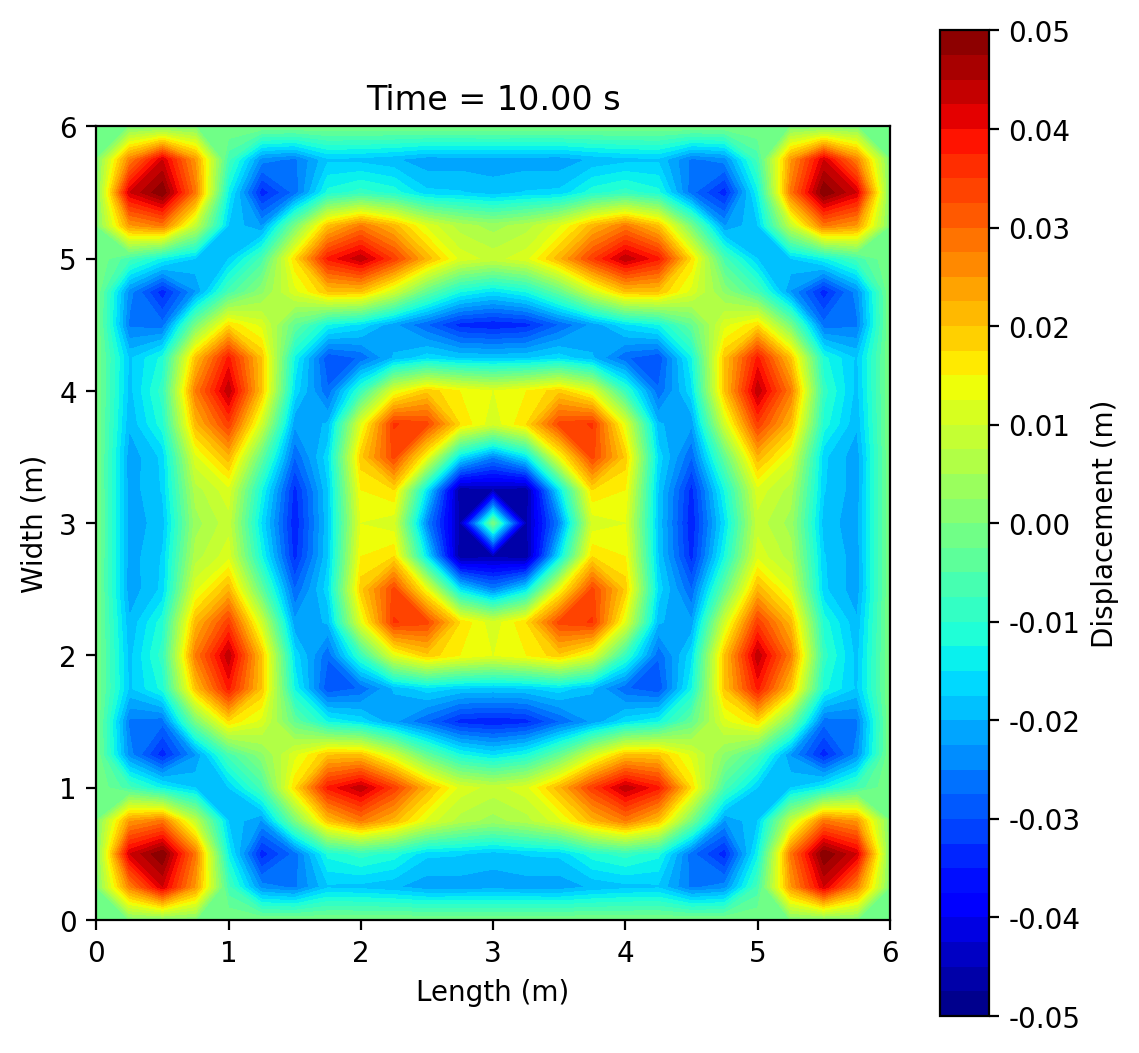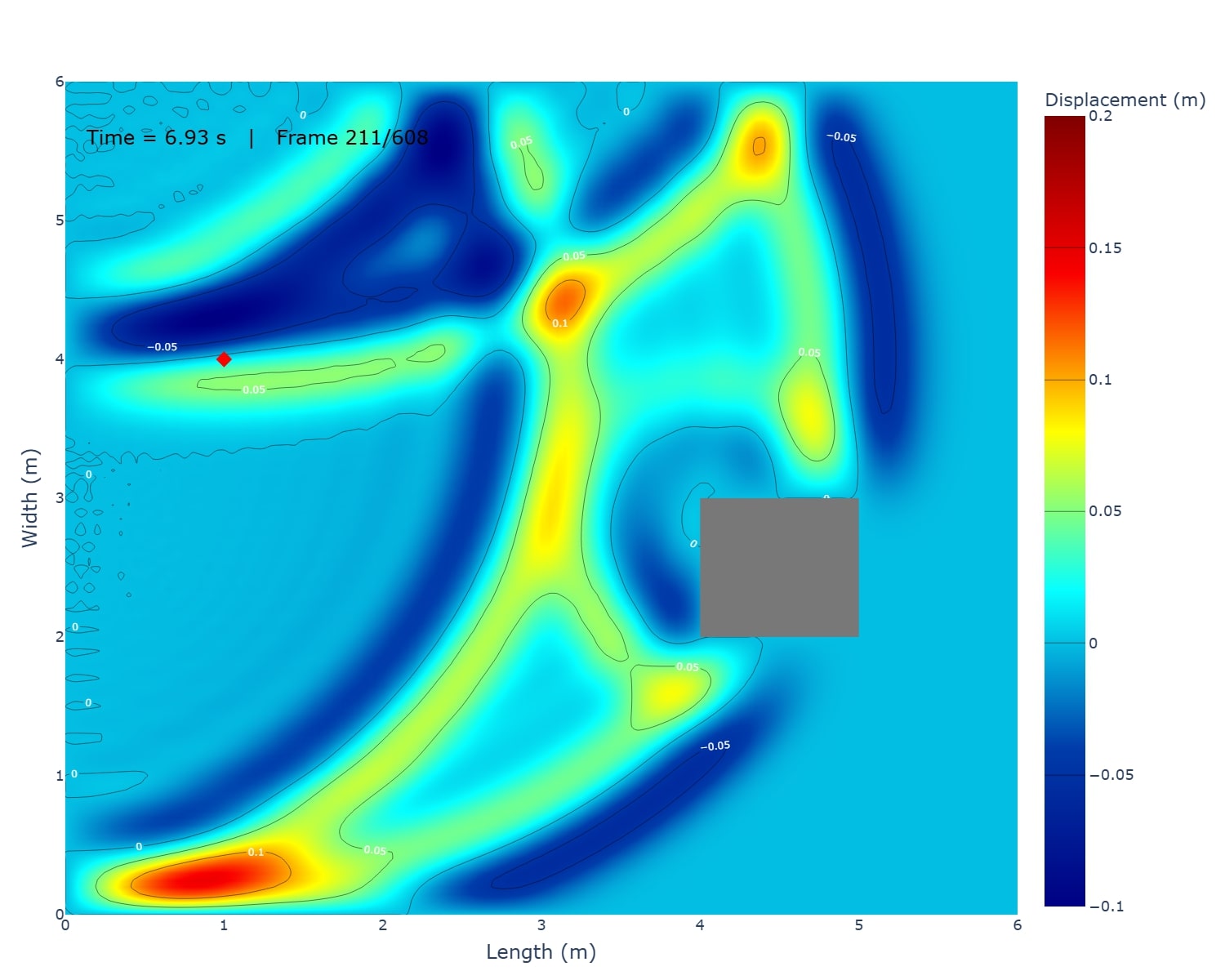
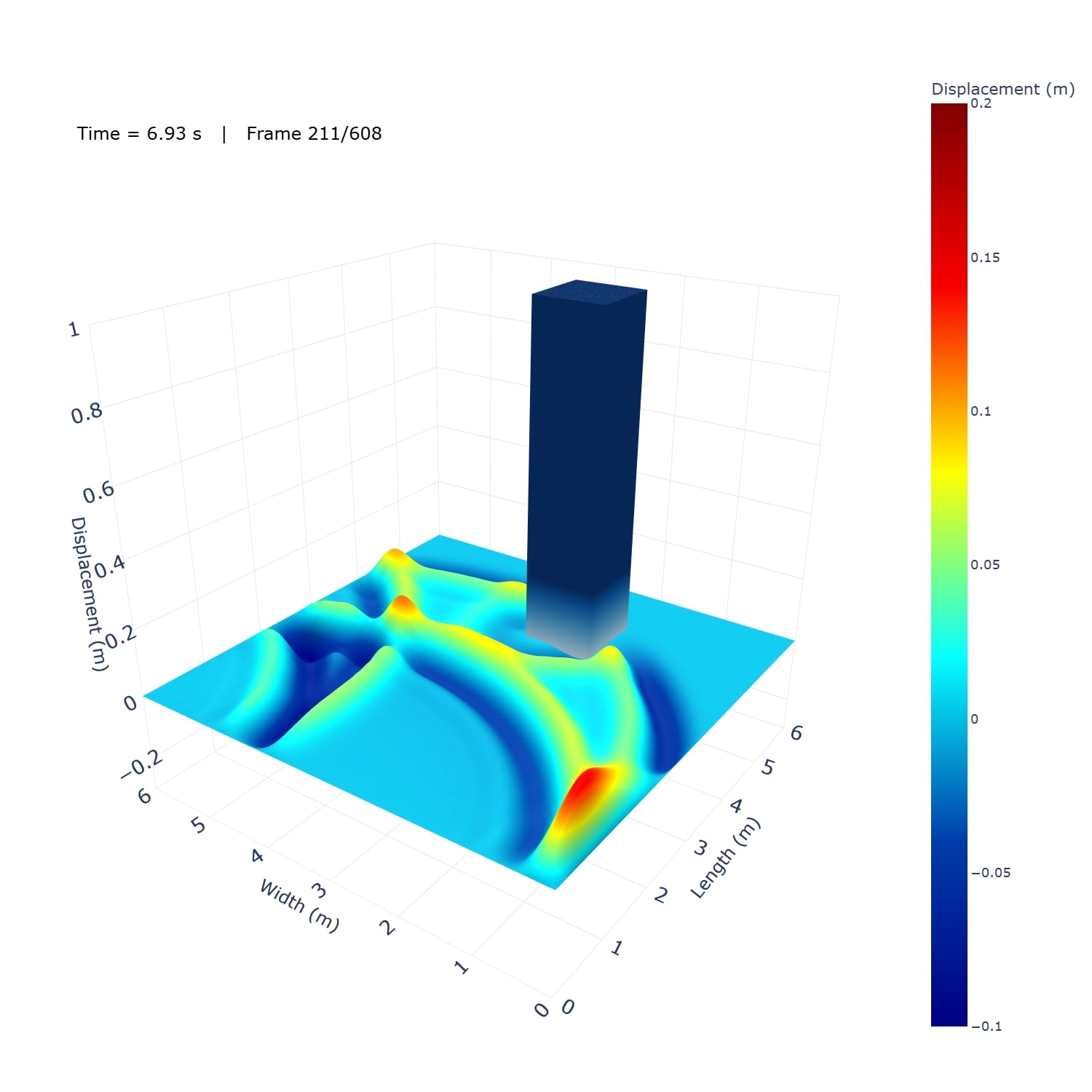
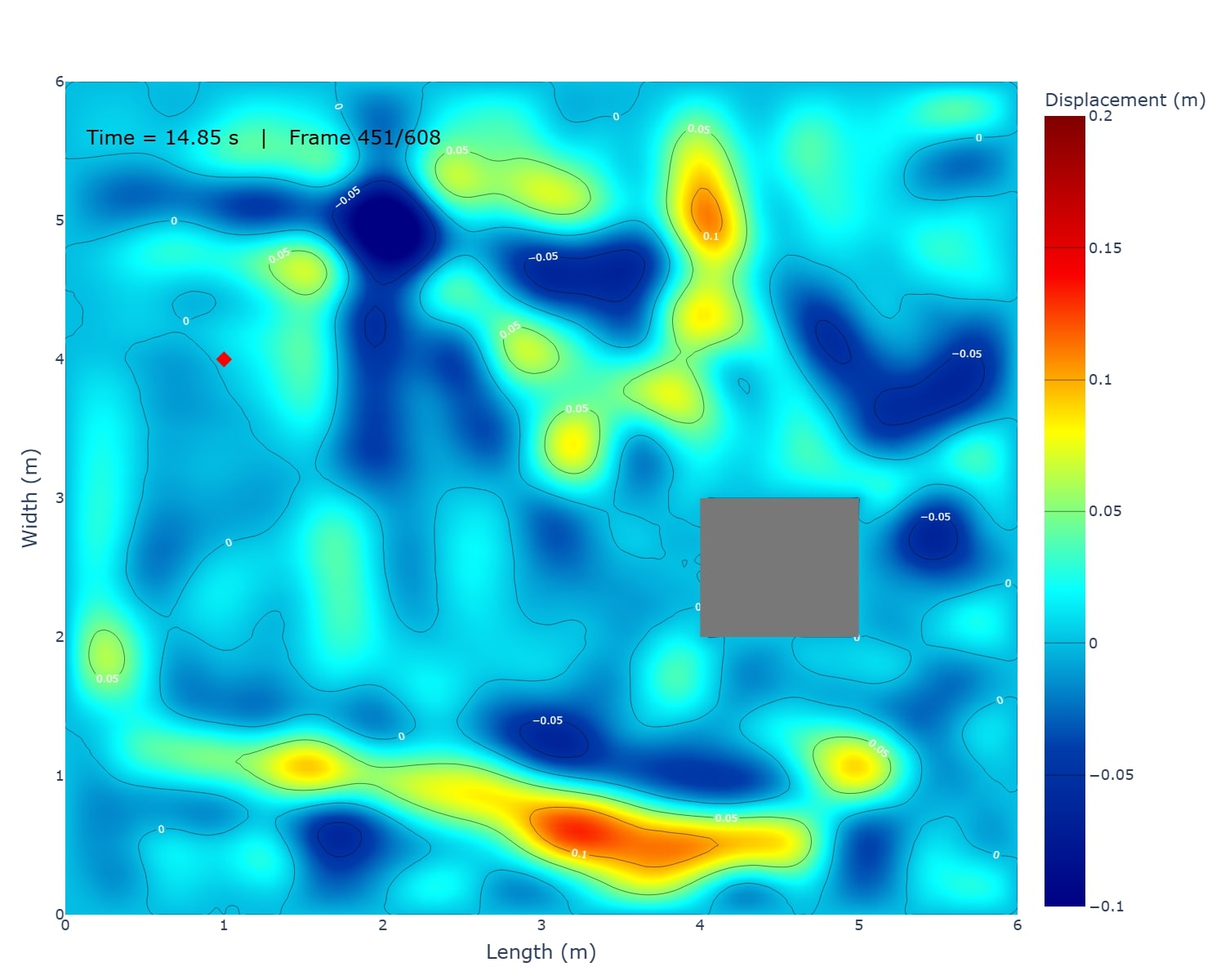
This project simulates 2-D surface waves on a 6 m × 6 m water domain by solving the wave equation ztt = c2(zxx + zyy) with fixed (zero-displacement) edges using an explicit finite-difference scheme. A short pulse (or sinusoid) at a chosen point generates circular ripples that reflect from the boundaries and form interference patterns; an optional rectangular pillar demonstrates scattering and “shadowing.” Results are shown as animated 3-D surfaces and 2-D contour maps, with brief mesh-refinement studies to illustrate numerical accuracy.